Решающее дерево (Decision tree)

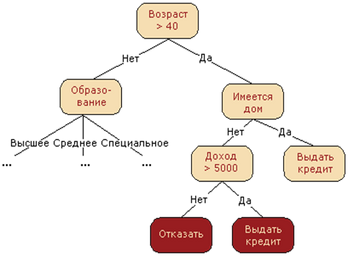
Решающее дерево (Decision tree) — решение задачи обучения с учителем, основанный на том, как решает задачи прогнозирования человек. В общем случае — это k-ичное дерево с решающими правилами в нелистовых вершинах (узлах) и некотором заключении о целевой функции в листовых вершинах (прогнозом). Решающее правило — некоторая функция от объекта, позволяющее определить, в какую из дочерних вершин нужно поместить рассматриваем объект. В листовых вершинах могут находиться разные объекты: класс, который нужно присвоить попавшему туда объекту (в задаче классификации), вероятности классов (в задаче классификации), непосредственно значение целевой функции (задача регрессии).

Чаще всего на практике используются двоичные решающие деревья.

Идея

немного Соколовщины и интуиции

Алгоритм построения

В корне дерева — рассматриваем всю обучающую выборку.

1. Проверить критерий останова алгоритма. Если он выполняется, выбрать для узла выдаваемый прогноз, что можно сделать несколькими способами.
2. Иначе требуется разбить множество на несколько не пересекающихся. В общем случае в вершине $t$ задаётся решающее правило $Q_{t}(x)$, принимающее некоторый диапазон значений. Этот диапазон разбивается на $R_t$ непересекающихся множеств объектов, $S_{1},S_{2},\dots ,S_{R_{t}}$, где $R_t$ — количество потомков у вершины, а каждое $S_i$ — это множество объектов, попавших в $i$-го потомка.
3. Множество в узле разбивается согласно выбранному правилу, для каждого узла алгоритм запускается рекурсивно.

Решающие правила

Чаще всего в качестве $Q_{t}(x)$ берут просто один из признаков, то есть $x^{i(t)}$.

Традиционные разбиения на диапазоны:

• $S_{t}(j)=\left\{x\in \mathbb {X} :h_{j}\leq x^{i(t)}\leq h_{j+1}\right\}$ для выбранных $h_{1},\dots ,h_{j+1}$
• $S_{t}(1)=\left\{x\in \mathbb {X} :\langle x,v\rangle \leq 0\right\};S_{t}(2)=\left\{x\in \mathbb {X} :\langle x,v\rangle >0\right\}$ — по сути проверка угла.
• $S_{t}(1)=\left\{x\in \mathbb {X} :\rho (x,x_{0})\leq h\right\};S_{t}(2)=\left\{x\in \mathbb {X} :\rho (x,x_{0})>h\right\}$, где расстояние $\rho$ определено в некотором метрическом пространстве (например,$\rho(x, y) = |x - y|$).
• $S_{t}(1)=\left\{x\in \mathbb {X} :x^{i(t)}\leq h\right\};S_{t}(2)=\left\{x\in \mathbb {X} :x^{i(t)}>h\right\}$ — предикаты, $\langle x,v\rangle$ — скалярное произведение векторов.

В целом, взять можно любые решающие правила, но лучше — интерпретируемые, поскольку их легче настраивать. Особого смысла брать что-то сложнее предикатов нет, так как уже с их помощью можно получить дерево со 100%-й точностью на обучающейся выборке (но при этом и скорее всего переобучиться).

Выбор оптимального решающего правила

Считаем, что решаем задачу многоклассовой классификации или регрессии в $R$-ичном дереве.

Обычно для построения дерева выбирается целое семейство решающих правил. Чтобы найти среди них оптимальное для каждого конкретного узла, требуется ввести некоторый критерий оптимальности. Для этого вводят некоторую меру $\mathrm {I} (t)$ измерения того, насколько разбросаны объекты (регрессия) или перемешаны классы (классификация) в некотором узле $t$. Эта мера называется критерием информативности.

Затем для каждого варианта решающего правила подсчитывается мера того, насколько будут разбросаны объекты (регрессия) или перемешаны классы (классификация) при таком разбиении:

$\Delta \mathrm {I} (X_{t},t)=\mathrm {I} (X_{t},t)-\sum _{i=1}^{R}\mathrm {I} (X_{t_{i}},t_{i}){\frac {N(t_{i})}{N(t)}}$, где $R$ — на сколько узлов разбивается узел, $t$ — текущий узел, $t_{1},\dots ,t_{R}$ — узлы-потомки, получающиеся при выбранном разбиении, $N(t_{i})$ — количество объектов обучающей выборки, попадающие в потомок $i$, $N(t)$ — попавших в текущий узел, $X_{t_{i}}$ — объекты, попавшие в $t_i$-ую вершину.

$\Delta \mathrm {I} (X_{t},t)$ также называется Information gain, то есть сколько информации мы получим при таком разбиении. Для выбора решающего правила требуется взять argmax от неё по всевозможным признакам и параметрам семейства решающих правил. При таком взятии мы как раз и получим оптимальное разбиение множества объектов в текущей вершине.

Критерии останова

Лекции Соколова (6 стр.)

• Ограничение максимальной глубины дерева.
• Ограничение минимального числа объектов в листе.
• Ограничение максимального количества листьев в дереве.
• Останов в случае, если все объекты в вершине относятся к одному классу.
• Требование, что Information gain при дроблении улучшался как минимум

на $s$ процентов.

Выбор прогноза в листе

Самый простой способ — взять самый часто встречающийся класс среди объектов обучающей выборки, попавших в этот лист, для классификации или среднее целевых функций этих объектов для регрессии.

В задачах классификации c $k$ классами в листе $t$ также можно хранить вероятности классов — например, по классической вероятности: $\mathbb {P} (y=y_{i}|x)={\dfrac {\#{X_{t}}}{N(t)}}$, где $\mathbb {Y} =\{y_{1},y_{2},\dots ,y_{k}\}$ — классы. Более подробно, как в таком случае выбирать класс, описано в обработке пропусков

Если задана матрица штрафов, то есть в случае несимметричных потерь, можно минимизировать штраф и взять в качестве класса в листе $\hat{y}$: ${\hat {y}}={\underset {y\in \mathbb {Y} }{\operatorname {argmin} }}\sum _{i}\lambda _{y_{i}y}$, где $\lambda _{y_{i}y}$ — элементы матрицы штрафов.

В регрессии — использовать функцию потерь, то есть:

${\hat {y}}={\underset {y\in \mathbb {Y} }{\operatorname {argmin} }}\sum _{i}L(y,y_{i})$

Выбор функции потерь в общем случае является параметром алгоритма.

Прогнозирование

Для случая отсутствия пропущенных значений. Алгоритм: начиная с корня, применить к новому объекту решающее правило. Таким образом определяется, в какой потомок объект должен "попасть", и рекурсивно запустить этот процесс для него.

Сложность прогнозирования для одного объекта для полностью построенного дерева — $O(h)$, где $h$ — высота дерева. Вообще говоря, дерево может быть несбалансированным, поэтому оценка в $O(\log N)$, где $N$ — размер тренировочной выборки, не гарантируется.

Метод обработки пропущенных значений

Лекции Воронцова, 59-я минута.

Сергей Иванов: Вроде в билетах этого нет, но вполне вопрос.

При обучении дерева объекты с пропущенными значениями у признака, по которому идет разбиение, игнорируются: $\Delta \mathrm {I} (X_{t},t)\approx {\dfrac {\#\{x\in X_{t}:x_{i(t)}{\mbox{not missing}}\}}{N(t)}}\cdot \Delta \mathrm {I} (\{x\in X_{t}:x_{i(t)}{\mbox{not missing}}\},t)$

При построении прогноза при необходимости разбить подвыборку в вершине $t$ по отсутствующему признаку происходит следующая процедура: будем как бы предполагать, что этот признак принимает случайное значение. Определим по обучающей выборке вероятности, с которой новый объект попадёт к каждому потомку — $w_{1},w_{2},\dots ,w_{R},w_{i}={\dfrac {N(t_{i})}{N(t)}}$. Затем отправим объект независимо к каждому потомку, получим прогнозы $y_{1},y_{2},\dots ,y_{R}$. В случае регрессии это будут непосредственно значения целевой функции, в случае классификации — вероятности принадлежности какому-то зафиксированному классу $y$(который, как будет видно ниже, надо перебирать): $y_{i}=\mathbb {P} (y|x,t_{i})$

Дальше можно поступать образом, схожим с выбором прогноза в листе: так, для регрессии можно просто объединить отклики с вероятностями в качестве весов, ${\hat {y}}=w_{1}y_{1}+\dots +w_{R}y_{R}$.

Пусть $t_0$ — корень дерева. В случае классификации ${\hat {y}}={\underset {y\in \mathbb {Y} }{\operatorname {argmax} }}\mathbb {P} (y|x,t_{0}){\overset {\mbox{def}}{=}}{\underset {y\in \mathbb {Y} }{\operatorname {argmax} }}\sum _{i=1}^{R}w_{i}\mathbb {P} (y|x,t_{i})$

CART-деревья

Реализация решающего дерева — за подробностями милости просим сюда.

Обобщающая способность деревьев

Для любой обучающей выборки существует дерево, которое не будет допускать на нём ни одной ошибки. Подобрать правильный критерий останова бывает затруднительно, поэтому прибегают к стрижке — строят дерево целиком, а затем начинают обрубать узлы с листов. Подробнее.